Bloom filters: Digging large sequence database

April 23, 2020 | 6 Minute Read

All notes derived from Dr. Vineet Bafna’s lecture. CSE283

Problem : Finding an Isoform From 1000 RNA-seq Experiments.

Say we want to find a particular isoform in RNA-seq experiments from 1000 different tissues. With 1 experiment having 20 Gb of reads, the total RNA-seq data will reach 20 Tb. Therefore it is impossible to fit 20 Tb of reads into memory, even with Burrow’s Wheeler transform (BWT). Alternatively, we can compress each RNA experiment into a shorter binary string. We can also compress our desired isoform using the same method. By comparing the binary strings, it might be faster to filter out the RNA-seq experiment of interest.

This method is called Bloom filter. It is a data structure designed to tell us if an element is present in a set in a rapid and memoru efficient way [1]. In our example, the element will be isoform of interest, and the set will be all reads of 1 RNA-seq experiment. Let’s borrow this brilliant idea from computer science and see how it works!

Steps of making Bloom Filters

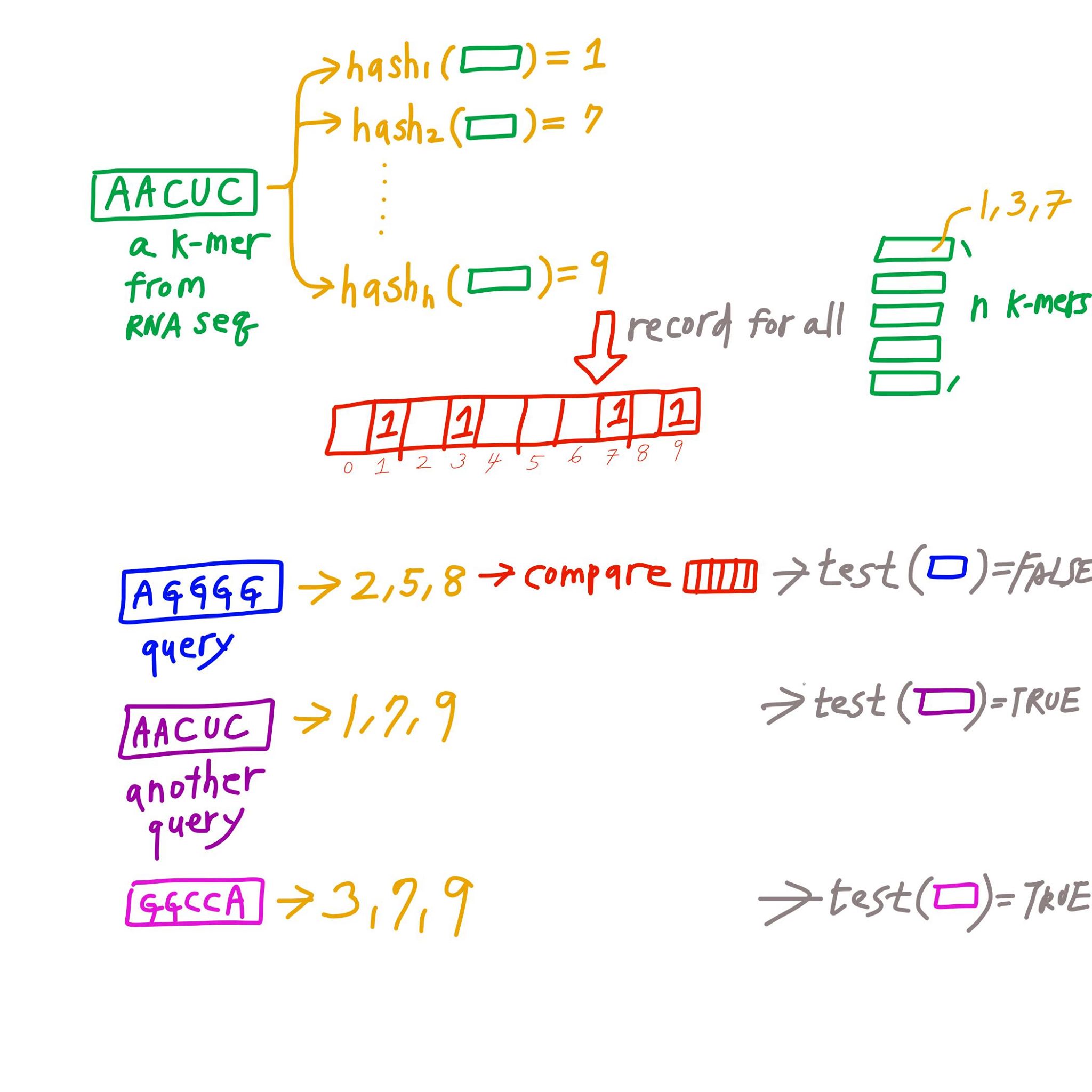
1. Find h different hash function that will convert a k-mer into a number between 1 to b of equal probability.
2. Construct a vector 0 of length b [0,0,0,.....0,0,0].
3. For all all k-mers in 1 RNA-seq experiment. Convert k-mer to number by the hash function, and record the number n by writing an 1 in the nth position of the vector.
4. Convert all k-mers in the isoform to number using the same function. And check if all of those positions are 1.
5. If all of the positions are 1 in the vector, then likely the isoform is in the database.
6. We can subsequently check by traditional analysis to confirm.

How Accurate of Bloom Filters?

It seems that there’s some chance that bloom filters can give you the wrong answers. For example, suppose bit 7,8,9 is the output after fitting the first k-mer of the isoform, even if 7,8,9 are 1 in the vector, we still cannot be 100% sure that they come from the same k-mers. Maybe there are some other kmers that produce 9,10,11 and the other producing 5,7,8. Therefore we need to choose the length of vector b and number of hash function h carefully to avoid such misunderstandings.

Let us first calculate some probability:

We denote test(o) as if all bits in position o from the b-bit vector are 1.

What is the probability of isoform in an RNA-seq experiment if test(o) = FALSE?

Zero. Because if isoform is in the experiment, then every k-mer produced by the hash function will occupy the same positions as the query.

What is the probability 1 k-mer of the isoform exist in an RNA-seq experiment if test(o) = TRUE?

Say we have $n$ k-mers in the RNA-seq experiments. Each of them will occupy $h$ bits. Because the way hash functions are designed, every bits has equal probability to be chosen. The probability of a bit not being chosen is $1-\frac{1}{b}$. After $n \times h$ chossing, the probability of a particular bit still being 0 is $q= (1-\frac{1}{b})^{nh}$. This can be approximate as $\exp(-nh/b)$

Let’s just pretend $q = \exp(-nh/b)$

The probability of a bit being 1 just by chance is $(1-q)$. For all $h$ bits to be hit by accident, the probability is $(1-q)^h$ (False Positive)

What False Positive Rate(FPR) Can you Tolerate?

Here you can choose whatever rate $p$ you can tolerate. Then all we do is to set $(1-q)^h < p$

Find h?

Assume number of k-mers $n$ and length of vector $b$ is constant, here we sought to minimize the equation $(1-\exp(-nh/b)^h$. To do it, take first derivate on $h$ and set it to zero, we get this:

when $h = \frac{b ln(2)}{n}$, FPR reaches minimum.

(The math is kinda tedious.)

Find b?

Plugging the $h$, we can get a threshold of $b > \frac{n ln(1/p)}{(ln(2))^2}$

False positive rate for the isoform

Above, we calculated for the false positve rate for 1 k-mer. But each isoform contains $l$ k-mers. Do we need all $l$ k-mers to match?

Let’s not be too stringent. Since with lower coverage, maybe the RNA-seq experiment does not have the whole length of the isoform. There will also be some seqencing errors in the dataset. If we require all k-mer to appear, then we will certainly miss a lot of RNA-seq experiments.

Let’s set up a rule: if fraction $\theta$ of bits fit, we decide isoform exist in that RNA-seq experiment. Should $\theta$ be 0.5? 0.7? or 0.99?

Within $l$ k-mers, we can expect $lp$ false k-mer matches. (With $p$ as the tolerable FPR you set for k-mer matches.) As long as the threshold is higher than k-mer FPR, that is $\theta > p$, our bloom filter can detect isoform appearance better then random.

Note: According to Chernoff bound, the probability of an event deviating from the expected value ($lp$ here) decrease exponentially as we deviate more. That is to say, we don’t need to worry about values a lot larger than $lp$ since they are rare.

A Real Example

Question:

We have an isoform of length $100$, setting $k=25$.

Sequencing error $\epsilon=0.05$.

We decide to tolerate FPR for k-mers $p=0.5$.

Choose parameter: (1) number of hash function $h$ per k-mer (2) length of binary vector $b$ (3) percent k-mer match $\theta$

Answer

Plug in $b > \frac{n ln(1/p)}{(ln(2))^2} = \frac{n}{ln(2)}$

Plug in $h = \frac{b ln(2)}{n} = 1$

For all k-mer to have sequencing error = $(1-\epsilon)^k ~ 0.6$.

Only $0.6$ of all k-mers will be correctly sequenced. So $\theta$ cannot be higher than this. $\theta < 0.6$

And we expect $0.5$ of k-mers can be false match. $\theta > 0.5$

Therefore we can set $\theta$ to be around $0.55$.

Searching Multiple Datasets: Bloom Trees [2]

Above we only dealt with 1 RNA-seq experiment. But we have $1000$ of them! Although making each of them a bloom vector already speed up a lot, some smart people still want it to be faster.

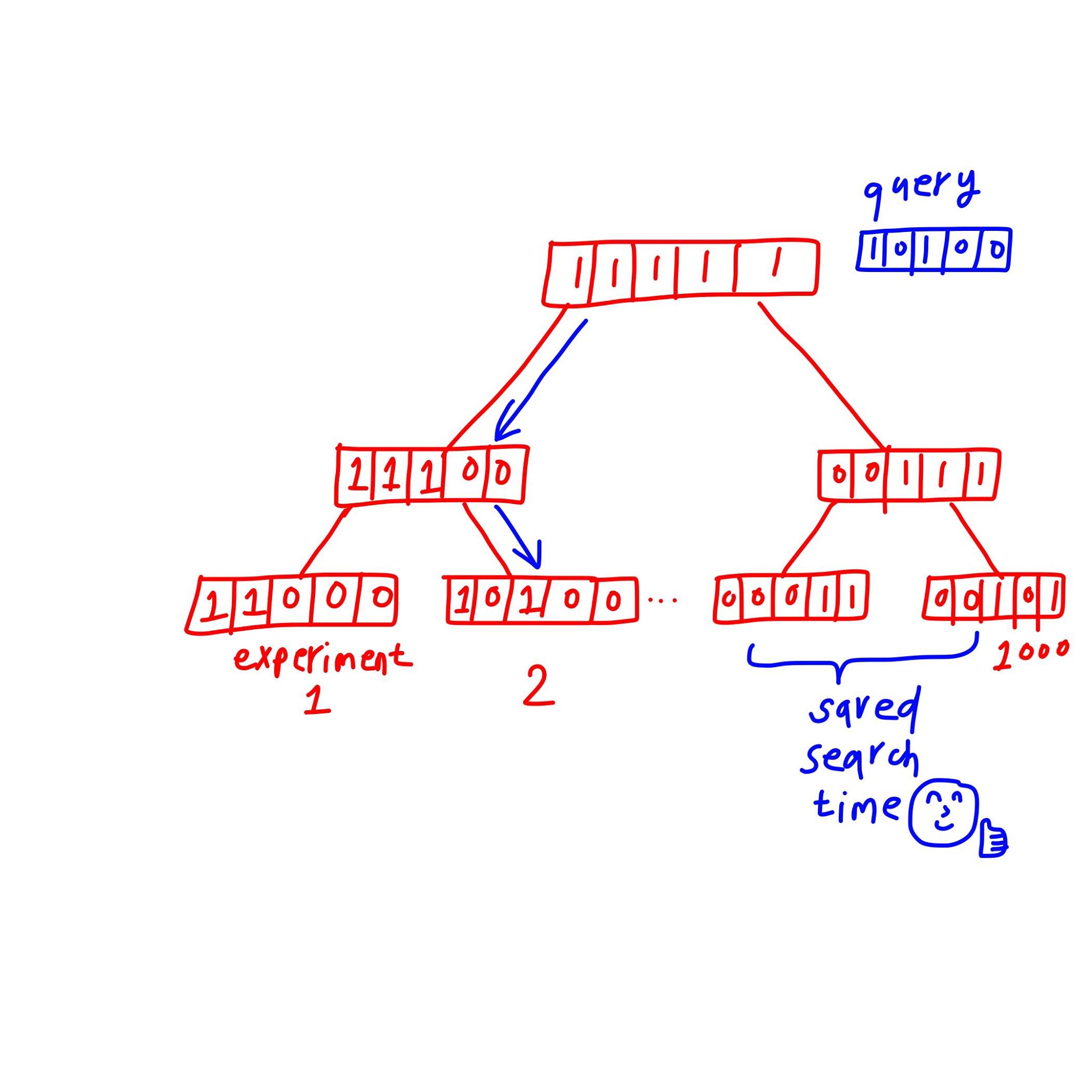
Think of the bits in the binary vector as a concise way to describe the composition of each experiment. So the union of two experiments can be presented as another bloom filter, with 1s from both filled. These people construct a tree of bloom filters, with parent nodes of 2 bloom filters as the union of the 1s. As we transverse the tree, the nodes we visit narrows down the number of filters we need to search by dividing us to either right or left path.

My Main Takeaway

Alignmment is an expensive way to extract feature from sequencing experiments. By compressing the k-mer compositions into binary vectors, we can speed up searching at the cost of accuracy. This only serve as a filter, to reduce the number of alignment needed confirm the existence of an isoform.

1. Bloom Filters by Example
2. Fast search of thousands of short-read sequencing experiments
3. CSE283